Symmetry Factors of Graphs

Particle physicists like to represent things with diagrams. The popular example is Feynman diagrams, and there are rules to draw and evaluate diagrams for different scattering processes. Diagrams also arise in the large scale structure of cosmology, where matter fluctuations can be described using perturbation theory (see this Wikipedia article).

Diagrams for cosmological perturbation theory (specifically large scale structure): they are basically functions of directed graphs. That is:

• The value of the diagram is the product of weights of edges and vertices.
• Each edge in the diagram is associated with a momentum flow, which enters through the vertices.
• The weight of and edge is a scalar function of the momentum flow in the edge.
• The weight of a vertex is a scalar function of the momentum flow in the edges connecting to the vertex.

These diagrams have two types of symmetry factors:

• The internal symmetry factor $-$ the number of topologically-invariant permutations of the edges of the graph.
• The external symmetry factor $-$ if the vertices are labeled, the number of permutations of vertices that produce topologically distinct graphs.

The Internal Symmetry Factor

The internal symmetry factor simply counts the number of ways we can connect the edges from each vertex together to form a given topology. Here's an example: suppose we have a graph we'll call $D_{321}$, with the topology ${ v_1 \textbf{ - } v_1 ,\, v_1 \textbf{ - } v_2 ,\, v_2 \textbf{ - } v_3 },$ where vertices are denoted $v_{1 - 3}.$ There are 6 configurations of edge connections that give the same topology:

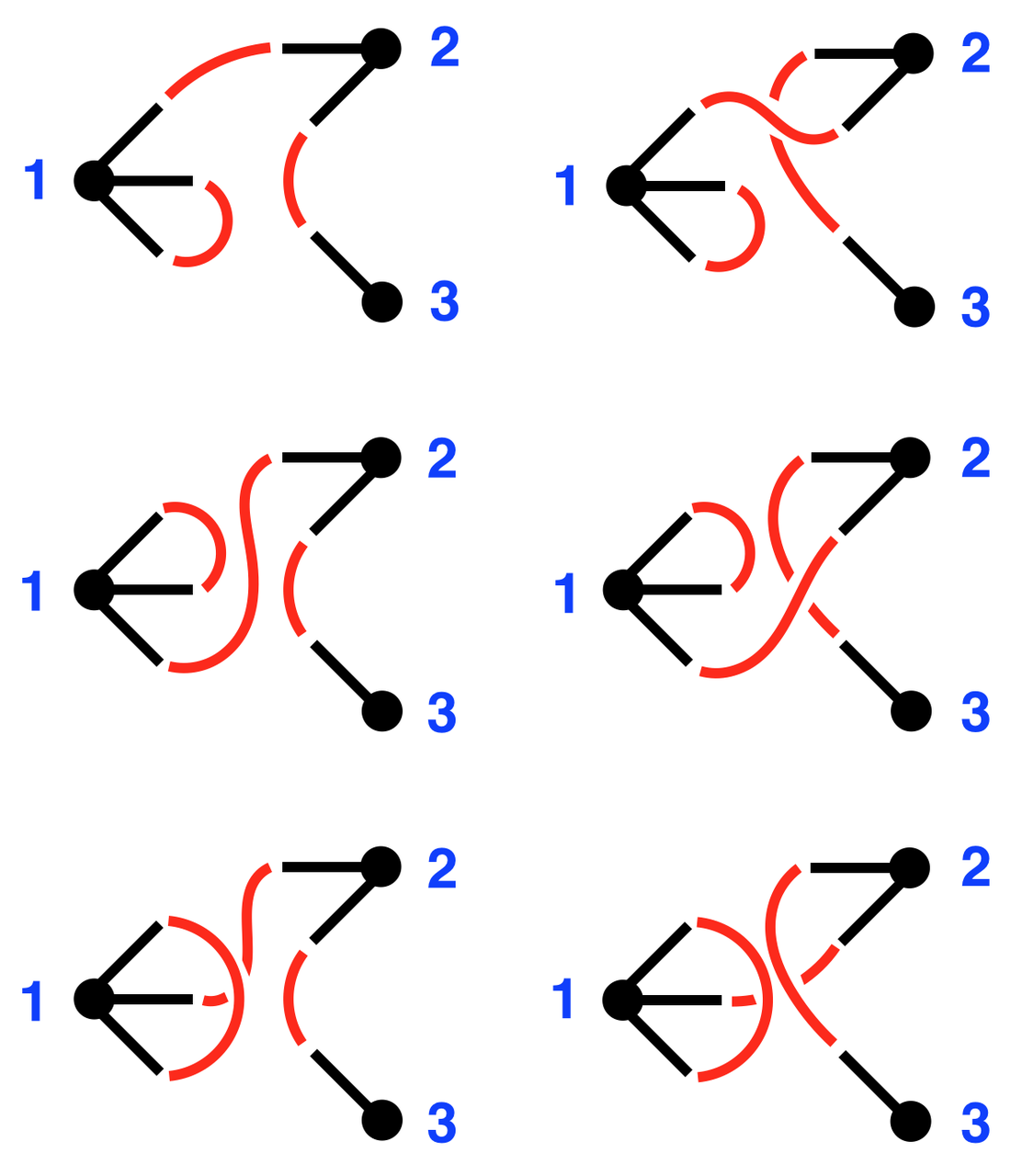
So the internal symmetry factor is $S(D_{321}) = 6.$ What is the symmetry factor for a general graph $D$ with $k$ vertices? Let's derive a formula.

There are two relevant quantities for a general graph:

$$ \begin{align} n_i &: \text{ the number of edges connecting to vertex } i. \\ n_{ij} &: \text{ the number of edges connecting vertex } i \text{ to vertex } j. \end{align} $$

Note $\sum_j n_{ij} = n_i$. First, let's take a simpler case first: $n_{ii} = 0$ for all $i$. For each vertex, let's define the multinomial coefficient

$$ M_i \equiv \dfrac{n_i!}{\prod_j n_{ij}!} \,, $$

which counts how many ways we can divide up the $n_i$ edges connecting to vertex $i$ into groups that go to each of the vertices. This tells us the symmetry factor contribution for each vertex, and now we need to multiply by the number of ways $C_{ij}$ to connect the set of edges running between each pair of vertices. But this is easy:

$$ C_{ij} = n_{ij}! $$

So the symmetry factor for graphs with $n_{ii} = 0$ is:

$$ S(D[n_{ii} = 0]) = \Bigl(\prod_{i = 1}^k M_i \Bigr) \Bigl( \prod_{i = 1}^k \prod_{j = 1}^{i-1} C_{ij} \Bigr) \,. $$

Now let's handle the case where there can be "tadpole" loops at a single vertex. Clearly the multinomial factor $M_i$ is still the same, since the vertices don't know where the edges are going. But now we need to include a term for $C_{ii}$, the number of way to connect $n_{ii}$ edges from a vertex to itself.

The edges from a vertex to itself are connected in pairs, so $C_{ii}$ is the number of ways to group $n_{ii}$ labeled objects into pairs. You may recognize this counting problem as giving a double factorial (it is equivalent to a perfect matching of a complete graph of $n_{ii}$ vertices, or countings of various types of binary trees). More explicitly, taking the first few cases of $n_{ii} = 2, 4, 6$ ($n_{ii}$ must be even), we get $C_{ii} = 1, 3, 15,$ and it's not hard to see

$$ C_{ii} = (n_{ii} - 1)!! $$

One can go through a more explicit combinatorial counting and see that

$$ C_{ii} = \frac{n_{ii}!}{(2!)^{n_{ii} / 2} (\frac12 n_{ii})!} = (n_{ii} - 1)!! $$

Therefore the internal symmetry factor for any graph is

$$ \boxed{ S(D) = \Bigl(\prod_{i = 1}^k M_i \Bigr) \Bigl( \prod_{i = 1}^k \prod_{j = 1}^{i} C_{ij} \Bigr) \,, } $$

where

$$ \boxed{ \begin{align} M_i = \frac{n_i!}{\prod_j n_{ij}!} \,, \ C_{ij} = \begin{cases} n_{ij}! & i \neq j \\ (n_{ii} - 1)!! & i = j \,. \end{cases} \end{align} } $$

If we apply this formula to the figure above, we have $M_1 = 3 ,\, M_2 = 2 ,\, M_3 = 1,\,$ and $C_{ij} = 1$ for all $i,\, j$, so that $S = 6$ as we the figure explicitly computed.

The External Symmetry Factor

The external symmetry factor counts how we may permute the vertex labels on the graph to produce a topologically distinct graph (think of the vertex labels as colors). For example, for a graph $D_{332}$, with the topology ${ v_1 \textbf{ - } v_2 ,\, v_1 \textbf{ - } v_2 ,\, v_1 \textbf{ - } v_3 ,\, v_2 \textbf{ - } v_3 },$ there are 3 distinct topologies, each having two equivalent vertex labelings:

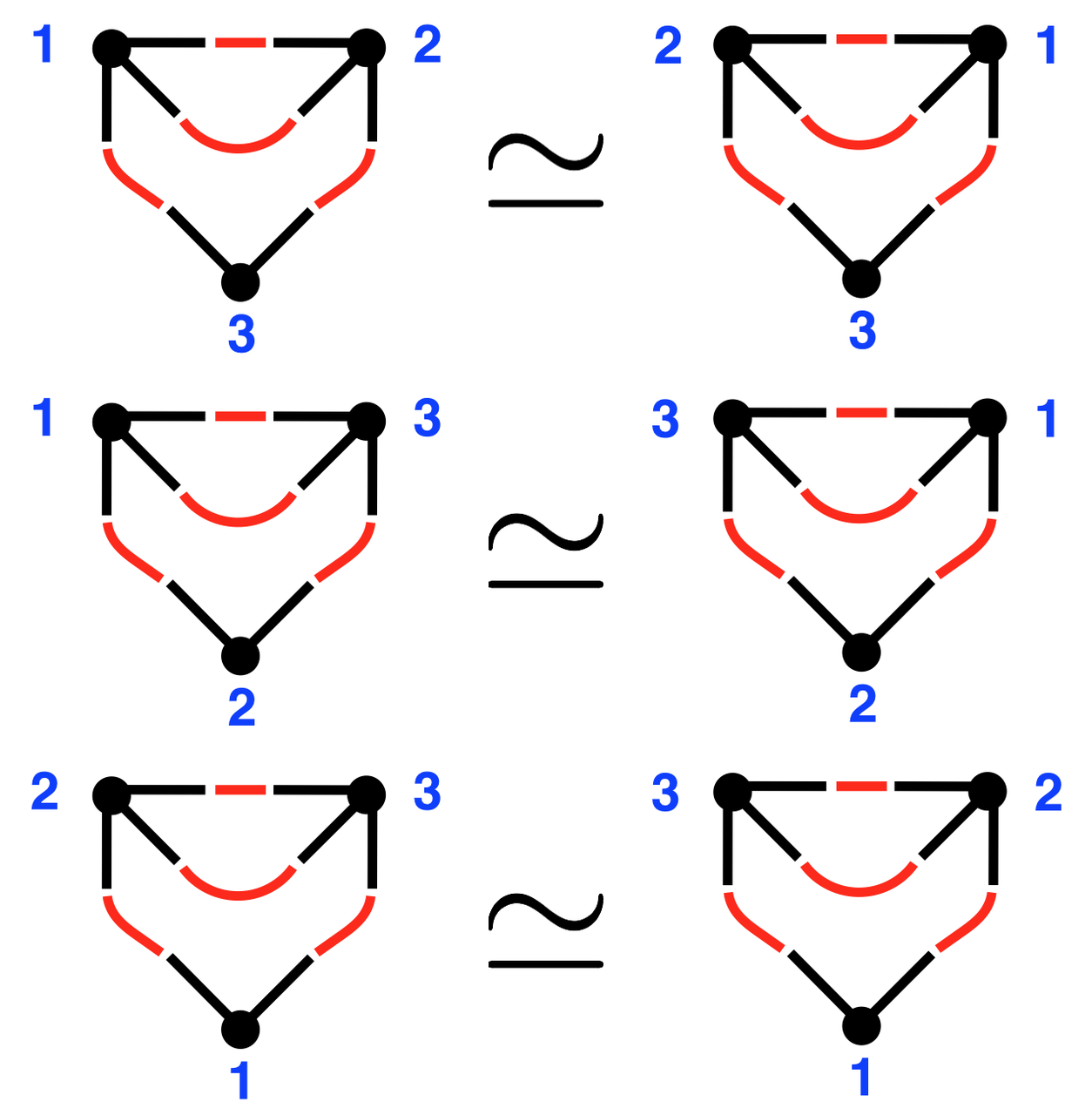
So the external symmetry factor $E(D_{332}) = 3$. This factor can be computed by using the adjacency matrix $A$, which encodes the $n_{ij}$:

$$ A_{ i j } = n_{ i j } \,. $$

The adjacency matrix for $D_{332}$ is distinct for the different rows of the figure:

$$ \left( \begin{matrix} 0 & 2 & 1 \\ 2 & 0 & 1 \\ 1 & 1 & 0 \end{matrix} \right) \,, \;\; \left( \begin{matrix} 0 & 1 & 2 \\ 1 & 0 & 1 \\ 2 & 1 & 0 \end{matrix} \right) \,, \;\; \left( \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 2 \\ 1 & 2 & 0 \end{matrix} \right) \,. $$

Therefore, the external symmetry factor is:

$$ \boxed{E(D) = \text{the number of unique adjacency matrices under permutation of the vertex labels.}} $$

There doesn't seem to be a simple formula for this, as it depends on the symmetry group of the graph, but one can straightforwardly calculate $E(D)$ using the adjacency matrix in code.

Great! Now we know how to compute various symmetry factors of graphs, and they use fun features of combinatorics.